[수학] 페리수열

[출처] http://navercast.naver.com/science/math/1049

야 구에서 타율은 타자가 얼마나 많은 안타를 칠 수 있는지를 알기 쉽게 소수로 나타낸 확률이다. 예를 들어 어떤 타자가 오늘까지 10번의 타석에 들어서 3번의 안타를 쳤다면 이 타자의 타율은 3/10= 0.3이므로 3할이다. 이 타자가 그 다음 날 4번의 타석에서 1번의 안타를 또 쳤다면 모두 14번의 타석에서 4번의 안타를 친 것이므로 타율은 4/14 ≈ 0.286 즉, 2할 8푼 6리라고 한다.

 

타율을 계산할 때는 '바보 셈'이 필요하다

 

위의 설명한  계산을 분수의 덧셈으로 나타내면 다음과 같다.

 

 

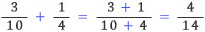
이 분수의 덧셈이 어딘가 이상하다고 느끼셨는지? 초등학교 수학시간에 배운 대로 옳게 분수의 덧셈을 하면 다음과 같다.

 

 

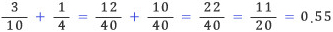
이렇게 계산하는 것이 옳은 분수의 덧셈이지만, 타율을 계산할 때는 앞서 설명한, 분수의 틀린 계산 방법대로 계산하여야 한다.  이렇게 야구에서 타율을 계산하기 위해 분수의 덧셈을 할 때 분모는 분모끼리 분자는 분자끼리 더하는 셈을 ‘바보 셈’이라고도 한다. 수학적으로 옳지 않은 바보 셈을 이용할 경우 편한 때가 있는 것이다.

 

 

'바보 셈'을 이용하여 만들어진 특별한 수학, 패리수열

 

이 바보 셈을 이용하면 특별한 수학을 만들 수 있다. 영국의 지질학자였던 존 패리(John Farey)는 1816년에 Philosophical Magazine이라는 잡지에 어떤 수열에 관한 글을 실었다. 이 수열은 0과 1 사이에 있는 분수를 나타내는 것으로 나중에 패리수열이라고 불리게 되었다.  n번째 패리수열을 F_n이라고 하면 0부터 1 사이의 기약분수들 중에서 분모가 n이하인 분수들을 순서대로 배열한 것이다. 예를 들어 1부터 7까지의 패리수열은 다음과 같다.

 

 

n번째 패리수열에서 a/b와 c/d가 이웃한 분수이고 a/b < c/d라면 두 분수의 차이는 항상 1/bd이므로 다음이 성립한다.

 

 

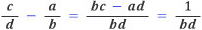
즉, bc-ad=1이다. 또 두 분수 a/b와 c/d사이에 있는 분수 p/q에 대하여 다음과 같은 바보 셈이 성립한다.

 

 

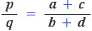
이를 테면, F₇에서 2/3과 3/4사이에는 5/7이 있다.  

 

 

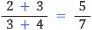
패리 수열을 좌표 평면에 나타내면 이웃한 분수가 이웃한 직선이 된다

 

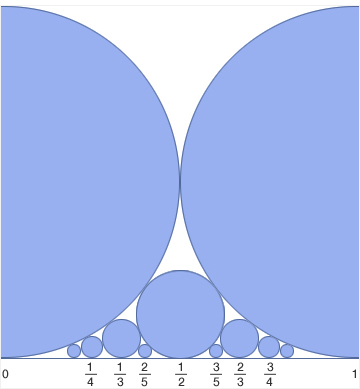
패리수열은 기하학과도 밀접한 관련이 있다. 먼저 좌표평면 위에 패리수열에 나타난 분수들을 표시해 보자. 분수를 좌표평면 위에 나타낼 때, 분모는 x축에 분자는 y축에 대응하여 점을 찍어 보자. 예컨데, 6번째 패리수열은 다음과 같다.

 

 

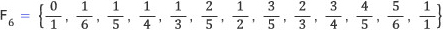
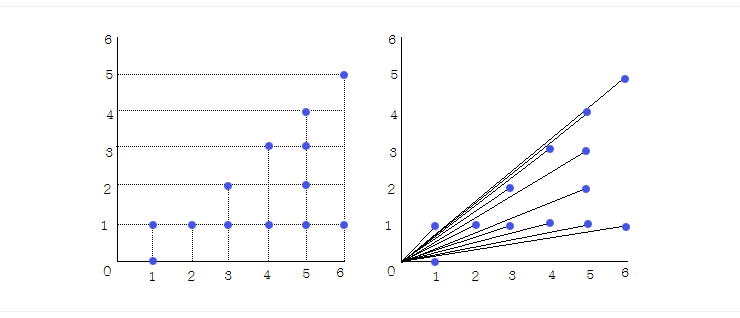
이를 좌표평면 위에 나타내면 아래 왼쪽 그림과 같고, 원점에서 이 점에 직선을 그으면 오른쪽 그림과 같다.

 

 

각각의 분수들은 이와 같이 얻어진 직선의 기울기와 같다. 특히 이웃했던 두 분수는 좌표평면에서도 인접한 두 직선으로 나타난다.     패리 수열로 만들어진 포드의 원   패리수열에 대한 또 다른 기하학으로는 포드의 원이라는 흥미로운 기하학이 있다. 즉, 패리수열에 나타난 분수 p/q에 대한 원 C(p/q)를 포드의 원이라고 하는데, 원 C(p/q)의 반지름과 중심은 다음과 같다.

  

포드의 원은 미국의 수학자 포드(Lester R. Ford)의 이름을 딴 것으로 그는 1938년 American Mathematical Monthly에 이 원에 대한 논문을 실었다. 포드의 원의 흥미로운 점은 첫 번째 패리수열 F1에 의하여 만들어진 두 개의 반원은 접하고 F2에 의하여 만들어진 두 반원과 한 개의 작은 원도 서로 접한다. 이와 같이 n번째 패리수열 Fn에 의하여 만들어진 포드의 원은 서로 접한다는 것이다. 특히 어떤 원도 다른 원과 교차하는 경우는 없다.   예를 들어 패리수열 F5에서 포드의 원 C(2/5)는 두 개의 포드의 원 C(1/3), C(1/2)과 접한다. 또 F7에서는 두 개의 포드의 원 C(1/3,) C(3/7) 과 접한다. 다음 그림은 패리수열에서 몇 개의 분수에 대한 포드의 원을 그린 것이다.

 

 

수학은 틀린 것에서도 새로운 분야가 개척되는 학문   패리수열은 매우 흥미로운 특성 때문에 오늘날에도 지속적으로 연구되고 있으며, 많은 수의 논문들이 계속 발표되고 있다. 초등학교 수학시간에 옳지 않다고 배운 분수에 대한 바보 셈이 놀랍고 재미있는 수학이 될지 누가 알았을까? 이처럼 수학은 틀린 것에서 조차도 새로운 분야가 개척되는 학문이다.

 

 

 

 

---------------------------------------------------------------------------------------

패리수열이 정규교과과정에는 나오지 않지만 널리 알려져있는 수열이라는데.. 왜 난 존재자체조차 몰랐을까;;;;

재미있네~